Hello guys, welcome back to our blog. Here in this article, I will discuss how to select the right solver for code generation in Simulink, and what are the types of solvers.

Ask questions if you have any electrical, electronics, or computer science doubts. You can also catch me on Instagram – CS Electrical & Electronics

Also, read:

Choosing Right Solver For Code Generation

Simulink, a powerful simulation and modeling tool developed by MathWorks, is widely used for simulating dynamic systems, particularly in engineering disciplines like automotive, aerospace, and electrical engineering. One of the most important aspects of Simulink modeling is selecting the right solver. The solver is the computational engine that dictates how the system’s equations are solved over time. The correct solver selection can significantly impact the efficiency, accuracy, and performance of your simulations and generated code.

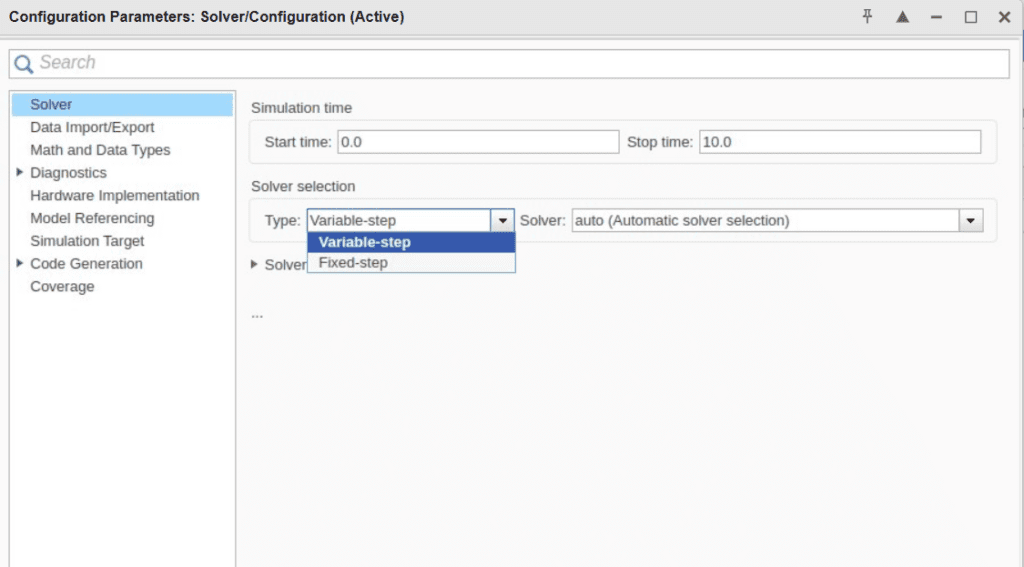
In Simulink, there are two primary types of solvers you can choose from: Fixed-Step and Variable-Step solvers. These solvers are designed to handle different types of simulation scenarios, and understanding when to use each is crucial for achieving optimal results in your models.

This article will provide an in-depth comparison of Fixed-Step and Variable-Step solvers, exploring their advantages, use cases, and implications for real-time simulations and code generation. We will also guide you through selecting the right solver based on your specific modeling needs.

Understanding Fixed-Step Solvers

Fixed-step solvers are computational algorithms that use a constant step size to solve the model’s differential equations over time. This means that no matter how the system behaves, the time between successive simulation steps remains the same throughout the simulation

Advantages of Fixed-Step Solvers

01. Predictability: The constant step size allows for highly predictable behavior during simulations. This predictability is especially important for real-time simulations, where the timing between each simulation step must be consistent and known in advance.

02. Determinism: In real-time and embedded system applications, where precise timing is critical, Fixed-Step solvers offer deterministic results. The solver’s step size ensures that every computation takes the same amount of time.

03. Ease of Debugging: Since the step size is constant, debugging can be easier because the system’s state changes at regular intervals. This predictability makes it simpler to analyze the behavior of the system step-by-step.

Use Cases for Fixed-Step Solvers

Fixed-Step solvers are ideal in situations where time accuracy and consistency are crucial. They are commonly used in the following cases:

Real-Time Simulations: In applications such as hardware-in-the-loop (HiL) testing, where the simulation must occur at a specific, constant rate to communicate with physical systems.
Embedded Systems: When generating code for embedded systems, the fixed-step approach ensures that the simulation time step corresponds to the time step of the microcontroller or processor, which is crucial for timing-sensitive applications.
Control Systems: When modeling control systems that interact with hardware, using a fixed step can guarantee synchronization between the model and the control algorithm.

Examples of Fixed-Step Solvers

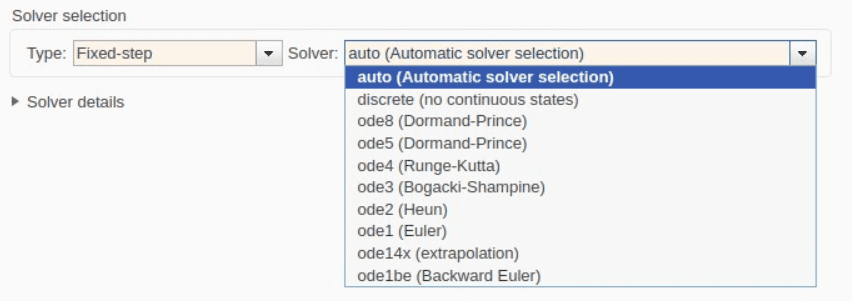
Some commonly used Fixed-Step solvers in Simulink include:

ode1 (Euler): A simple, first-order solver using the Euler method. This solver is generally used when a rough approximation is sufficient and efficiency is a priority over accuracy.
ode4 (Runge-Kutta): A higher-order solver that provides better accuracy than the Euler method and is commonly used in control system simulations.

Understanding Variable-Step Solvers

Variable-step solvers, unlike fixed-step solvers, adjust the simulation step size based on the behavior of the model. These solvers decrease the step size when the system exhibits rapid changes and increase the step size when the system behaves more smoothly. The solver adapts to the dynamics of the system, balancing between computation efficiency and accuracy

Advantages of Variable-Step Solvers

01. Efficiency: Variable-Step solvers are more efficient than Fixed-Step solvers because they automatically adjust the step size based on the system’s requirements. If the system is behaving smoothly, the solver increases the step size, reducing computational effort. Conversely, if the system’s dynamics change rapidly, the solver reduces the step size to capture the behavior accurately.

02. Accuracy: These solvers are particularly useful when dealing with systems that have fast-changing dynamics or require higher accuracy in certain regions of the simulation. The solver adjusts to maintain an optimal balance between accuracy and performance.

03. Flexibility: Variable-step solvers can handle a wide range of system behaviors, making them versatile for simulating complex systems with nonlinear or time-varying characteristics.

Use Cases for Variable-Step Solvers

Variable-step solvers are ideal in scenarios where the system’s dynamics can change rapidly or are not predictable. They are often used in the following situations:

Non-Real-Time Simulations: For system-level modeling or when the simulation is not constrained by time or real-time requirements, Variable-Step solvers can be highly effective.
Design Simulations: In control system design, where accuracy in transient behavior is important but real-time execution is not critical.
System Analysis: When performing sensitivity analysis or studying the system’s behavior under various operating conditions.

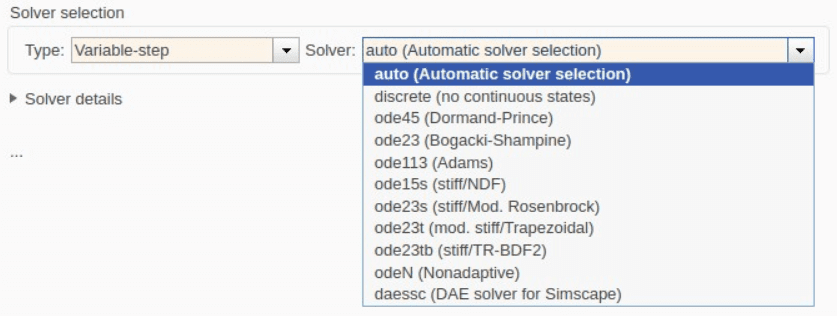
Examples of Variable-Step Solvers

Some widely used Variable-Step solvers in Simulink include:

ode45 (Dormand-Prince): A popular solver for general-purpose simulations that require a good balance of accuracy and performance. It is typically used for systems with smooth but nonlinear behavior.
ode23 (Bogacki-Shampine): A solver suited for less stiff systems where computational efficiency is a higher priority, but with adequate accuracy for most simulations.

Key Differences Between Fixed-Step and Variable-Step Solvers

To understand which solver is right for your model, let’s compare the key differences:

Feature	Fixed-Step Solvers	Variable-Step Solvers
Step Size	Constant, predefined step size.	Dynamic, adjusts based on system behavior.
Predictability	Highly predictable, making it suitable for real-time.	Less predictable, suitable for non-real-time simulations.
Efficiency	May be computationally inefficient, especially for complex systems.	More efficient as it adapts to the system’s needs.
Accuracy	Can be less accurate in systems with rapid dynamics.	Offers higher accuracy, especially for rapidly changing systems.
Real-Time Use	Ideal for real-time applications (e.g., embedded systems, HiL).	Dynamic adjusts based on system behavior.

Choosing the Right Solver for Your Model

When deciding which solver to use, several factors must be considered. These include the type of system you are modeling, the need for real-time simulation, computational resources, and the accuracy requirements.

Considerations for Fixed-Step Solvers

01. If your model is part of an embedded system or you plan to generate real-time code, Fixed-Step solvers should be your go-to choice. Their consistent step size ensures that the model operates within the timing constraints of the hardware.

02. If your system is relatively simple and doesn’t exhibit fast dynamics, Fixed-Step solvers may provide an efficient and predictable simulation.

Considerations for Variable-Step Solvers

01. If your system has complex dynamics that change over time, such as nonlinearities or rapid changes in behavior, Variable-Step solvers can offer better accuracy by adjusting the step size accordingly.

02. For non-real-time simulations, such as control design, system optimization, or analyzing specific operating conditions, Variable-Step solvers offer a good balance of performance and precision.

Selecting Solvers for Code Generation

When it comes to code generation, the choice of solver can significantly impact the quality and reliability of the generated code.

Why Fixed-Step Solvers Are Preferred for Code Generation

Real-time systems, such as embedded control units or hardware-in-the-loop (HiL) simulations, require highly deterministic behavior. Fixed-step solvers are essential in these cases because they offer predictable step sizes, making them suitable for systems that need to operate in real time.

In contrast, Variable-Step solvers are typically not recommended for real-time code generation because they can cause non-deterministic behavior, leading to challenges in real-time performance.

How Solver Selection Affects Code Generation

Determinism: For code generation, Fixed-Step solvers ensure that the generated code operates with predictable timing, which is essential for embedded systems. This is critical when interfacing with hardware or when timing constraints must be strictly adhered to.

Real-Time Constraints: When using Simulink Coder or Embedded Coder for generating code, the solver selection should be fixed-step, as these tools generate code that assumes a constant time step.

Types of Fixed-Step Solvers for Code Generation

When generating code, it’s not just about choosing a fixed-step solver but selecting the one that matches your application needs. Here are some common options and their best use cases:

01. Discrete Solver

This solver is used when the model consists entirely of discrete blocks or fixed-step sample times.
It is the simplest and most efficient solver for real-time code generation. Best suited for applications like digital control systems or applications that require direct mapping of discrete-time models to real-time tasks.

02. Fixed-Step ODE Solvers

These solvers are used for systems that include continuous states but require fixed-step behavior.

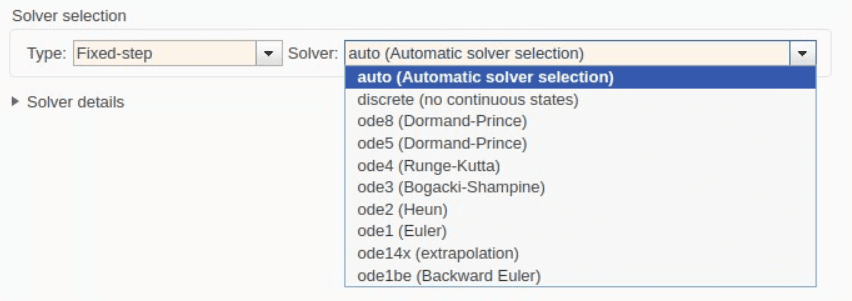
ode1 (Euler Method):

Computationally inexpensive and simple, but not highly accurate.
Used in scenarios where accuracy can be traded off for performance.

ode2 (Heun’s Method) and ode3 (Bogacki-Shampine):

Provide better accuracy than Euler but are more computationally expensive.
Suitable for slightly more complex systems.

ode4 (Runge-Kutta 4th Order):

A popular choice for systems that require a good balance of computational effort and accuracy.
Frequently used in control system models.

Key Considerations for Fixed-Step Solver Selection

Sampling Rate: The step size (or sampling rate) should align with the dynamics of your system. For fast-changing systems, a smaller step size ensures accuracy but increases computational load.
Use tools like the “solver profiler” in Simulink to test different step sizes and observe their impact on the simulation.

Task Synchronization: For multi-rate systems (e.g., models with components operating at different rates), ensure that the fixed-step solver step size accommodates the fastest rate as a common multiple of slower rates.

Real-Time Hardware Constraints: Ensure the step size allows the model to execute within the real-time constraints of your hardware. For example, microcontroller clock cycles or processor speed should be factored in.

Variable-Step Solvers in Non-Real-Time Applications

Variable-step solvers are often used during the early stages of design and testing because of their accuracy and flexibility. These solvers can help in:

Design Validation: When designing control algorithms or testing plant models, Variable-Step solvers allow you to focus on accuracy without worrying about the computational cost.
System-Level Modeling: Complex systems with nonlinear behaviors, such as hybrid powertrain models or robotics, benefit from the adaptability of Variable-Step solvers.

Popular Variable-Step Solvers

ode45 (Dormand-Prince):

Best for systems with smooth dynamics.
Balances computational cost and accuracy, making it suitable for initial system analysis.

ode23 (Bogacki-Shampine):

Efficient for less stiff systems but slightly less accurate than ode45.
Often used for faster, approximate simulations.

ode15s (Stiff Solver):

Handles stiff systems effectively, which occur in models with widely varying time constants, such as electrical circuits or chemical processes.

ode23t (Trapezoidal Rule):

Suitable for moderately stiff systems where accuracy is prioritized.

Drawbacks of Variable-Step Solvers in Code Generation

Non-Determinism: The dynamic nature of Variable-Step solvers makes them unsuitable for real-time systems.
Code Complexity: The code generated using Variable-Step solvers often lacks the determinism required for embedded systems, leading to potential execution issues.
Overhead: The solver’s continuous adaptation can increase computational overhead, making it impractical for systems with limited resources.

Best Practices for Solver Selection in Simulink

To master solver selection, consider the following tips:

01. Start with Variable-Step Solvers for Prototyping: During the initial stages of model development, use Variable-Step solvers to test the system’s behavior. They provide a good understanding of how your system responds to various conditions.

02. Switch to Fixed-Step Solvers for Real-Time Applications: Once the model is validated and you’re ready to implement it on hardware, switch to Fixed-Step Solvers. Ensure the step size is chosen carefully to balance between accuracy and computational efficiency.

03. Use Solver Profiler: Simulink’s Solver Profiler is an excellent tool for analyzing the performance of different solvers. It provides insights into the step size, solver performance, and computational cost, helping you make informed decisions.

04. Match Solver to Dynamics: For systems with slow dynamics, larger step sizes and simpler solvers (e.g., Euler) are sufficient. For systems with fast-changing or complex dynamics, smaller step sizes or higher-order solvers (e.g., ode4) are more appropriate.

05. Avoid Over-Sampling: While reducing the step size can improve accuracy, it can also lead to unnecessary computational burden. Strike a balance between accuracy and performance.

Common Pitfalls to Avoid

Ignoring Step Size in Fixed-Step Solvers: Choosing a step size too large can result in missed dynamics, while too small a step size can lead to excessive computational load.

Using Variable-Step Solvers for Real-Time Applications: Even though Variable-Step solvers are accurate, they should not be used for real-time or hardware-related applications due to their non-deterministic behavior.

Overcomplicating Models: Using a higher-order solver or excessively small step size for simple systems can waste computational resources.

Failure to Test in Real-Time Environment: Always test your Fixed-Step solver configuration in a real-time simulation or on the actual hardware before final deployment.

Conclusion

Solver selection in Simulink is a critical step that directly impacts the accuracy, efficiency, and real-time performance of your models. By understanding the differences between Fixed-Step and Variable-Step solvers and applying the guidelines outlined in this article, you can optimize your simulation and code generation workflow.

For code generation and real-time applications, Fixed-Step solvers are the gold standard, offering predictability and deterministic behavior. On the other hand, Variable-Step solvers are invaluable during the design phase, where flexibility and accuracy take precedence.

By mastering the art of solver selection, you can ensure that your Simulink models meet the highest standards of performance and reliability, whether you’re developing embedded systems, testing control algorithms, or performing system-level analysis.

This was about “Choosing Right Solver For Code Generation“. Thank you for reading.

Also, read:

About The Author

Chetan Shidling

Automotive | Technical Blogger | Engineer | Content Creator

See author's posts

Share Now