Data Structures And Algorithms Top Interview Questions And Answers
Hello guys, welcome back to my blog. In this article, I will discuss data structures and algorithms top interview questions and answers, the questions that I discuss in this article are most popularly asked in data structures and algorithms interviews.
If you have any doubts related to electrical, electronics, and computer science, then ask question. You can also catch me @ Instagram – Chetan Shidling.
Also, read:
- Types Of Data Analytics, Which Type Of Data Analytics You To Do.
- Tools For SEO Search Engine Optimization, How To Do SEO.
- High Salary Engineering IT Jobs, Companies Paying Huge Money.
Data Structures And Algorithms Top Interview Questions
Data structures and algorithms is a computer science engineering subject and it is a very important subject if you want to become a programmer. Almost in many companies data structures and algorithms questions are asked. Every tech company such as Google, Facebook, YouTube, LinkedIn, Accenture, Cognizant, etc will ask questions. Well, here in this article, I will discuss some popular questions and answers.
01. What is Data Structure and Algorithm?
A. Remember one thing data structure and algorithms using c language, Cpp, python, etc is not a language, a data structure is a concept set of algorithms used to structure the data, it is not a programming language such as like C, C++, Java, so there are just a set of algorithms, we are executing these algorithms using any programming language. The data structure means it is the collection of some data or elements and all possible operations which are required for those set of elements. For example: consider an array, where the set of elements is required to store in an array. Various operations such as inserting and deleting can be performed.
The computers are electronic data processing machines. In order to solve a particular problem we need to know: How to represent data in a computer, how to access them, and what are steps to be performed to get the needed output. These tasks can be achieved with the knowledge of data structures and algorithms.
02. What is difference between structure and unions?
A. The structure is defined as the collection of data of the same or different data types. All data items grouped are logically related and can be accessed using variables. The keyword used for structure is a struct. Related to structures, a union is a set of variables of different data types. The exclusive difference between a structure and a union is that in a state of unions, you can only store data in one field at any one time. To completely understand a union, imagine it as a chunk of memory that is used to store variables of different types. When a new value is allocated to a field, the current data is replaced with the new data.
Therefore, unions are used to save memory. They are beneficial for applications that require multiple members, wherever values need not be allotted to all the members at one time.
03. What is Time Complexity?
A. The time complexity of an algorithm represents the quantity of time needed by the algorithm to run to completion. Time requirements can be defined as a numerical function T(n), where T(n) can be measured as the number of steps, provided each step consumes constant time.
For example, the addition of two n-bit integers takes n steps. Consequently, the total computational time is T(n) = c*n, where c is the time taken for the addition of two bits. Here, we observe that T(n) grows linearly as the input size increases.
04. What is Space Complexity?
A. The space complexity of an algorithm describes the quantity of memory space needed by the algorithm in its life cycle. The space needed by an algorithm is equal to the sum of the following two elements.
A fixed part is a space needed to store certain data and variables, which are independent of the size of the problem. For example, constants used and simple variables, program size, etc.
A variable part is a space needed by variables whose size depends on the size of the problem. For example, dynamic memory allocation, recursion stack space, etc.
05. What is push, pop, stack overflow, stack underflow?
A. Push means adding element into an array, pop means deleting element from an array, stack overflow means the array is full, and stack underflow means the element is called from the array but it is empty.
06. What is linked list?
A. A linked list, in simple words, is a linear arrangement of data elements. Those data elements are described nodes. A linked list is a data structure which in turn can be employed to perform other data structures. Therefore, it serves as a building block to perform data structures so as to stacks, queues, and variations. A linked list can be seen as a train or a sequence of nodes in which each node includes one or more data fields and a pointer to the following node.
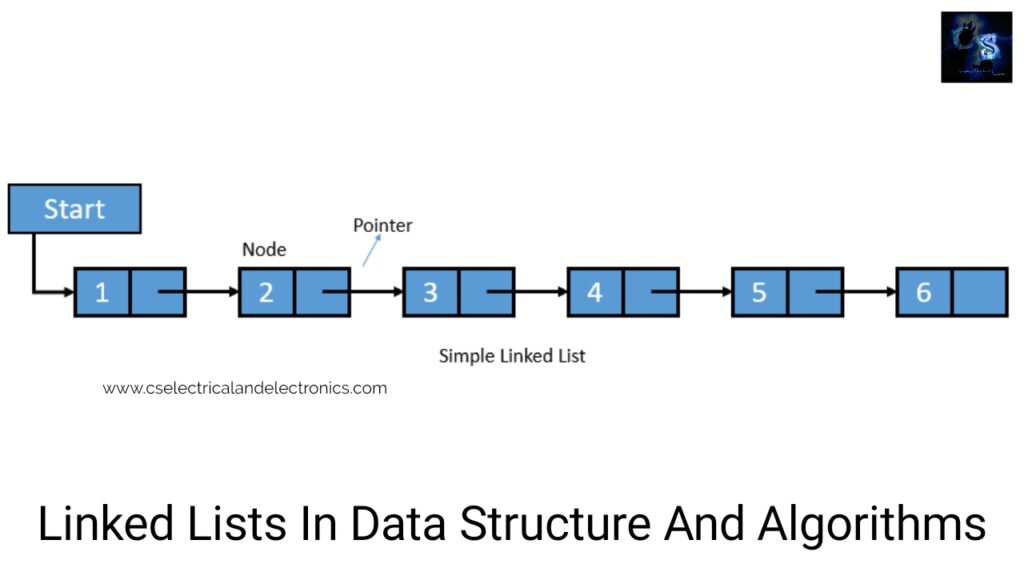
we can observe a linked list in which each node holds two parts, a data location and a pointer to the next node. The left portion of the node which holds data may include a simple data type, an array, or a structure. The right portion of the node contains a pointer to the next node (or address of the next node in order). Memory and the capacity of an array remain fixed. In the case of linked lists, we can keep adding and removing elements without any capacity constraints.
07. What are the different types of linked list?
A. The different types of linked list are:
Singly-linked lists: A singly linked list is the easiest variety of linked lists in which each node includes some data and a pointer to the next node of the corresponding data type. By assuming that the node contains a pointer to the next node, we determine that the node stores the address of the next node in the series. A singly linked list provides traversal of data just in one way.
Circular linked list: In a circular linked list, that last node holds a pointer to the first node of the list. While traversing a circular linked list, we can start at any node and traverse the list in either direction, forward or backward, till we reach the same node where we began. Therefore, a circular linked list has no beginning and no end.
Doubly linked list: A doubly linked list or a two-way linked list is a higher complex variety of linked list which includes a pointer to the next as well as the earlier node in the series. Hence, it consists of three parts—data, a pointer to the next node, and a pointer to the last node.
Circular doubly linked list: A circular doubly linked list or a circular two-way linked list is a more complex type of linked list that contains a pointer to the next as well as the previous node in the order. The difference between a doubly linked and a circular doubly linked list is identical as that exists between a singly linked list and a circular linked list.
Header linked list: A header linked list is a specific type of linked list which includes a header node at the start of the list. Hence, in a header linked list, START will not point to the first node of the list but START will include the address of the header node. The following are the two kinds of a header linked list: Grounded header linked list which saves NULL in the next field of the last node and circular header linked list which saves the address of the header node in the next field of the last node.
08. Difference between searching and sorting?
A. Searching means to determine whether a special value is now in an array or not. If the value is now in the array, then searching is assumed to be successful and the searching method gives the place of that value in the array. But, if the content is not being in the array, the searching method displays a relevant message and in this case, searching is assumed to be unsuccessful.
Sorting involves managing the elements of an array so that all are placed in some proper order which may be both ascending or descending. A sorting algorithm is specified as an algorithm that sets the elements of a list in a particular order, which can occur either numerical order, lexicographical order, or a user-defined order.
09. What are the different types of sorting algorithms?
A. The different types of sorting algorithms are:
- Bubble sort
- Insertion sort
- Selection sort
- Merge sort
- Quick sort
- Radix sort
- Heap sort
- Shell sort
- Tree sort
a. Bubble sort is a very easy method that sorts the array components by regularly moving the largest element to the highest index position of the array segment (in fact of arranging elements in ascending order). In bubble sorting, consecutive adjacent pairs of elements in the array are compared by each other. If the component at the lower index is greater than the component at the higher index, the two elements are interchanged so that the component is placed before the bigger one. This process will remain till the list of unsorted elements exhausts.
b. Insertion sort is a very easy sorting algorithm in which the sorted array (or list) is made one element at a time. The main idea behind insertion sort is that it inserts each part into its proper place in the final list. To save memory, most implementations of the insertion sort algorithm performance is by moving the current data element past the already sorted values and frequently interchanging it with the preceding value until it is in its correct place. Insertion sort is less effective as compared to other more advanced algorithms such as quicksort, heap sort, and merge sort.
c. Selection sort is a sorting algorithm that has a quadratic running time complexity of O(n2), whereby making it ineffective to be used on big lists. Although selection sort does worse than the insertion sort algorithm, it is recorded for its simplicity and also has performance benefits over more complicated algorithms in certain circumstances. Selection sort is generally used for sorting files with very large objects (records) and small keys.
d. Merge sort is a sorting algorithm that practices the divide, conquer, and combine algorithmic model. Divide involves partitioning the n-element array to be sorted into two sub-arrays of n/2 components. If A is an array holding zero or one component, then it is already sorted. But, if there are more components in the array, divide A into two sub-arrays, A1 and A2, all containing about half of the components of A. Conquer involves sorting the two sub-arrays recursively. Combine involves merging the two sorted sub-arrays of size n/2 to provide the sorted array of n elements.
e. Quicksort is a broadly used sorting algorithm revealed by C. A. R. Hoare that offers O(n log n) comparisons in the average case to sort an array of n elements. However, in the worst case, it has a quadratic running time given as O(n2). Primarily, the quick sort algorithm is faster than other O(n log n) algorithms, because its effective implementation can reduce the probability of requiring quadratic time. Quicksort is also identified as a partition exchange sort.
f. Radix sort is a linear sorting algorithm for integers and does the concept of sorting names in alphabetical order. When we have a list of sorted names, the radix is 26 (or 26 buckets) because there are 26 letters in the English alphabet. So radix sort is also recognized as bucket sort. Observe that words are first sorted according to the first letter of the name. That is, 26 classes are utilized to arrange the names, where the first-class stores the names that start with A, the second class contains the names with B, and so on.
When radix sort is done on integers, sorting is done on each of the digits in the number. The sorting procedure proceeds by sorting the least significant to the most significant digit. While sorting the numbers, we have ten buckets, each for one digit (0, 1, 2, …, 9) and the number of passes will depend on the length of the number having a maximum number of digits.
10. What is tree and types of trees?
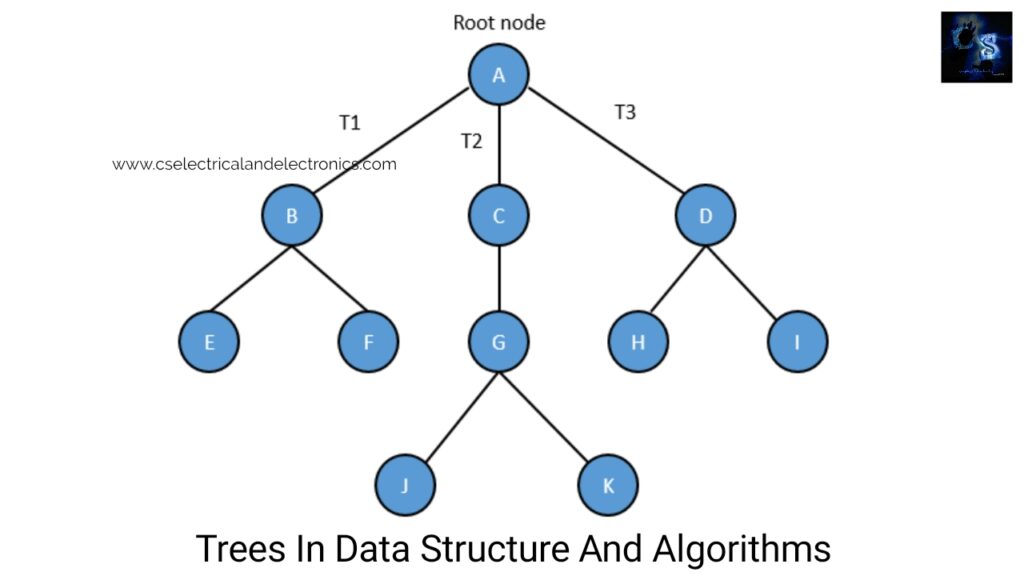
A. One tree is represented as a set of one or more nodes where one node is designated as the root of the tree and all the surviving nodes can be partitioned into non-empty sets any of which is a sub-tree of the root. Image shows a tree where node A is the root node and nodes B, C, and D remain children of the root node and set sub-trees of the tree rooted at node A.
Types of trees
- General trees
- Forests
- Binary trees
- Binary search trees
- Expression trees
- Tournament trees
11. What is queue and types of queues?
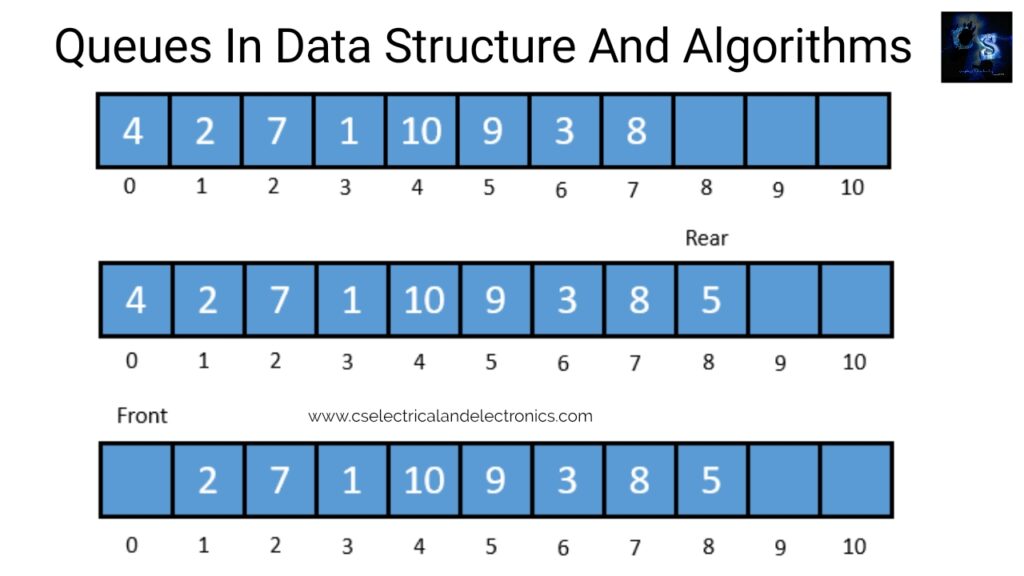
Assume we require to add another element by value 5, then REAR would be incremented by 1 and that value would be saved at the position pointed by REAR. The queue after addition would be as shown in block 02. Here, FRONT = 0 and REAR = 8. Each time a different element has to be added, we replicate the same procedure. If we need to delete a component from the queue, later the value of FRONT will be incremented. Deletions are made from just this end of the queue. The queue after deletion will be as shown in block 03.
Types of queue
- Circular Queues
- Deques
- Priority Queues
- Multiple Queues
12. What is Hashing and Collision?
A. A hash function is a mathematical formula that, when utilized to a key, generates an integer that can be utilized as an index for the key in the hash table. The main purpose of a hash function is that elements should be moderately, randomly, and uniformly distributed. It provides a unique set of integers within some proper range in order to decrease the number of collisions.
Collisions happen when the hash function maps two separate keys to the same location. Clearly, two records cannot be stored in the same location. Hence, a method used to solve the problem of collision, also called collision resolution technique, is applied. The two most common methods of resolving collisions are:
- Open addressing
- Chaining
13. How to calculate time complexity of the algorithm?
A. The time complexity of an algorithm represents the quantity of time needed by the algorithm to run to completion. Time requirements can be defined as a numerical function T(n), where T(n) can be measured as the number of steps, provided each step consumes constant time.
For example, the addition of two n-bit integers takes n steps. Consequently, the total computational time is T(n) = c*n, where c is the time taken for the addition of two bits. Here, we observe that T(n) grows linearly as the input size increases.
14. Difference between linked list and array?
A. Memory and the capacity of an array remain fixed. In the case of linked lists, we can keep adding and removing elements without any capacity constraints. A linked list can be seen as a train or a sequence of nodes in which each node includes one or more data fields and a pointer to the following node.
15. Difference between tree and graph?
A. A tree is recursively defined as a set of one or more nodes where one node is designated as the root of the tree and all the remaining nodes can be partitioned into non-empty sets each of which is a sub-tree of the root.

The above image shows a tree where node A is the root node; nodes B, C, and D are children of the root node and form sub-trees of the tree rooted at node A.
A graph is an abstract data structure that is used to implement the mathematical concept of graphs. It is basically a collection of vertices (also called nodes) and edges that connect these vertices. A graph is often viewed as a generalization of the tree structure, where instead of having a purely parent-to-child relationship between tree nodes, any kind of complex relationship can exist.
16. Applications of data structures and algorithms?
A. The computers are electronic data processing machines. In order to solve a particular problem we need to know: How to represent data in a computer, how to access them, and what are steps to be performed to get the needed output. These tasks can be achieved with the knowledge of data structures and algorithms.
Used in e-commerce websites, social media, YouTube, Facebook, and every software application needs data structures and algorithms.
17. What is binary search tree?
A. A binary search tree, also known as an ordered binary tree, is a variant of a binary tree in which the nodes are arranged in an order.
18. What is abstract data type?
A. In C, an abstract data type can be a structure held without regard to its implementation. It can be considered as a ‘description’ of the data in the structure by a list of operations that can be implemented on the data within that structure. The end-user is not concerned about the aspects of how the methods carry out their tasks. They are only knowledgeable of the ways that are available to them and are only concerned about calling those techniques and getting the outcomes. They are not concerned about how they operate.
19. Difference between quick and merge sort?
A. Primarily, the quick sort algorithm is faster than other O(n log n) algorithms, because its effective implementation can reduce the probability of requiring quadratic time. Quicksort is also identified as partition exchange sort.
Merge sort is a sorting algorithm that practices the divide, conquer, and combine algorithmic model. Divide involves partitioning the n-element array to be sorted into two sub-arrays of n/2 components. If A is an array holding zero or one component, then it is already sorted. But, if there are more components in the array, divide A into two sub-arrays, A1 and A2, all containing about half of the components of A. Conquer involves sorting the two sub-arrays recursively. Combine involves merging the two sorted sub-arrays of size n/2 to provide the sorted array of n elements.
20. What is the time complexity of different algorithms?
A. The time complexity of different algorithms are:
a. Linked list:
- Singly-linked lists – O(n)
- Circular linked list – O(n)
- Doubly linked list – O(n), and removal via a pointer is O(1)
b. Sreaching
- Linear search – O(n)
- Binary search – O(log n)
- Interpolation search – O(log2(log2 n)) for the average case, and O(n) for the worst case
- Jump search – O(√ n)
c. Queues
- Circular Queue – O(1)
- Deque – O(1)
- Priority Queue – O(log N)
d. Sorting
- Bubble sort – O(n2)
- Insertion sort – O(n + f(n))
- Selection sort – O(n2)
- Merge sort – O(n*log n)
- Quicksort – O(n log n) in the best case, and O(n2) in the worst case.
I hope this article “Data Structures And Algorithms Top Interview Questions And Answers” may help you all a lot. Thank you for reading.
Also, read:
- 100+ C Programming Projects With Source Code, Coding Projects Ideas
- 1000+ Automotive Interview Questions With Answers
- 1000+ Interview Questions On Java, Java Interview Questions, Freshers
- App Developers, Skills, Job Profiles, Scope, Companies, Salary
- Applications Of Artificial Intelligence (AI) In Renewable Energy
- Applications Of Artificial Intelligence, AI Applications, What Is AI
- Applications Of Data Structures And Algorithms In The Real World
- Array Operations In Data Structure And Algorithms Using C Programming