What Is Space Complexity, Calculation, Example, Big O Notation

Hello guys, Welcome back to our blog. Here in this article, we will discuss what is space complexity, how space complexity is calculated, examples, and what are Big O notation, Omega notation, and Theta notation in space complexity.

If you have any electrical, electronics, and computer science doubts, then ask questions. You can also catch me on Instagram – CS Electrical & Electronics.

Also, read the following:

What Is Space Complexity

Algorithm Analysis is the study of providing theoretical estimation for the required resources of an algorithm to solve a specific computational problem, which translates to calculating efficiency.

The efficiency of a program depends on the input length(which is the number of steps), known as time complexity, and the volume of memory, known as space complexity.

In programming, space complexity is a form of algorithm analysis that quantifies the amount of space taken by an algorithm to run as a function of the length of the input, or to put it in even simpler terms, it is the memory required by an algorithm to execute a program and produce output.

Now, Space Complexity is often expressed in big O notation, such as O(n), O(log(n)), O(n^2), and more., where n is the input size in n units of bits needed to represent the input data.

Significance of Space Complexity

A program requires memory for:

Storing constant values
Storing variable values
Storing program instructions

But all the above parts of a program take space and many times that space is usually not efficient in any manner thus, space complexity is used to determine the program form with the lowest amount of memory space taken up, which results in improved efficiency.

Auxiliary Space

Now, there is another memory allocated by the user’s program to solve the program problem which is known as Auxiliary Space. Auxiliary Space simply put is extra or temporary space and it is a part of Space Complexity and is in no way a part of input size.

Thus, Space Complexity = Input Space + Auxiliary Space

Method for calculating Space Complexity

Space Complexity = Input Size + Auxiliary Space

Now, here what happens is that even if the Input Size and Auxiliary Space take up a certain fixed memory size of the program thereafter, no matter what data values are placed inside the input size the memory size will stay the same. To explain this in elaborate let’s take up an example:

Program – Addition of 2 numbers

[  function add(n1, n2)
   {
        sum = n1+n2
        return sum
    }                               ]

Now, in the above program, if the user had to estimate the actual size of the program, he/she could do it by calculating the size the variables would take.

Let’s assume that the integer n1 took 2bytes, n2 took 2 bytes, and the sum variable took 6 bytes. Now, let’s assume that the auxiliary space is taken by the overhead which are the instructions such as “function” in the program and the “return” statement and assumes that these assumed constant statements took 8 bytes.

So, if we were to calculate the estimated total it would come out to 18 bytes. Now, no matter what is the values of n1 and n2, the variables will occupy 8 bytes only. And the entire program would occupy 18 bytes only and so it will be a constant space. This constant space or constant behavior is represented by O(1).

**Method for calculating Space Complexity**

Thus, the final result will be O(1) because it is a constant as no matter the value the user is giving of the input the size that the program is occupying will be more or less 16 bytes only, hence this program can be considered as O(1) Space Complexity Program.

Big O notation

The Big-O notation describes an asymptotic upper bound. It represents the program’s scalability(the measure of the program’s ability to increase or decrease in performance and cost in response to changes in the program and the processing demands of the system) and performance of the program.

To put it in simpler terms, Big O notation is used to make things simpler, by simply ignoring things that become irrelevant as n(the input data) gets large.

Examples of Big O notation:

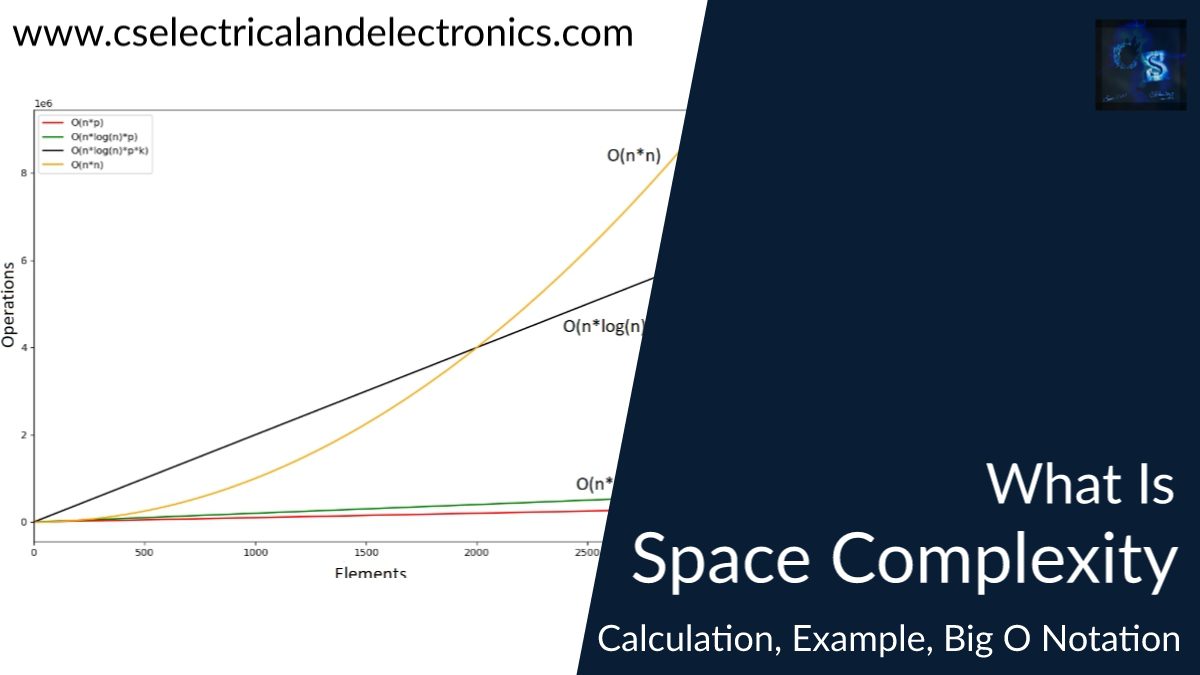
01. Constant Space Complexity – O(1)

In this Space Complexity, the amount of size taken by the program is constant irrespective of the input size of the program.

No matter what values, are placed inside the input the space size will remain the same. And, hence the Complexity will remain constant throughout.

02. Logarithmic Space Complexity – O(logn)

In this Space Complexity, the amount of data space taken by the program will be proportional to the log of the input size. When a recursive call is made, all current variables get placed on the stack and new ones are created. If the number of recursive calls increases logarithmically, i.e. n(input size) is halved with every recursive call, then the space complexity will be O(logn).

03. Linear Space Complexity – O(n)

In Linear Space Compleacity, the amount of data space taken by the program is directly proportional to the input size.

04. Quasilinear Space Complexity – O(n logn)

Quasilinear Space Complexity grows proportionally to the input size and a logarithmic factor. Given a data set of size n, the algorithm executes an n number of operations where each operation runs in log n (logarithmic) time.

05. Square Space Complexity – O(n^2)

In Square Space Complexity the space complexity grows proportionally to the square of the input size.

Omega notation – Ω

Now, other than Big O notation there is also an Omega notation Ω.

Omega notation Ω expresses an asymptotic lower bound of the running time of the program. This notation gives the best-case scenario of a program’s complexity which is completely different from Big O notation which gives the worst-case scenario of a program.

Big O notation is meaningful because it tells the user that their program will never be slower than a specific bound, and so it provides valuable information so that the user can argue that their program is good enough. If the opposite is done and the program is modified to make it better and find out about the complexity of the resulting program, the notation Ω is used.

Omega notation gives the user a complexity that the user knows the program won’t be better than. This is useful if the user wants to prove that a program runs slowly or an algorithm is a bad one. This can be useful to argue that an algorithm is too slow to use in a particular case. For example, saying that an algorithm is Ω( n³ ) means that the algorithm isn’t better than n³.

It might be Θ( n³ ), as bad as Θ( n⁴ ), or even worse, but we know it’s at least somewhat bad. So Ω gives us a lower bound for the complexity of our algorithm.

The reason you don’t typically see big-Omega bounds is that they’re notoriously tough to prove. The most notable example of a big Omega bound is the comparison sort lower bound of Omega(n log n), which gets cited a lot. A lot of algorithms on arrays also have trivial Omega(n) lower bounds.

Theta Notation – θ

The Theta notation expresses a function that is within lower and upper bounds. The reason you will typically see big-O, and not big-Theta, bounds for programs is because those bounds are repeatedly not tight. It isn’t correct that those bounds are necessarily big-Theta bounds. They often aren’t.

They will frequently either be the best-known bound or a simplification of the best-known bound. However, just because it is the programmer’s best-known bound doesn’t mean it matches the Omega bound (the requirement for being Theta).

This was about “What Is Space Complexity“. I hope this article may help you all a lot. Thank you for reading.

Also, read:

About The Author

Chetan Shidling

Automotive | Technical Blogger | Engineer | Content Creator

See author's posts

Share Now